
Simplify 4 5 6 2 3 8 3 7 12
Click here👆to get an answer to your question ️ Simplify 3√(2)2√(3)3√(2)2√(3) √(12)√(3)√(2) Solve Study Textbooks Guides Join / LoginWelcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102
Simplify (√3+2)(√3-2)
Simplify (√3+2)(√3-2)-Accurate answer to the question Simplify completely 2 √(3) ·4 √(21) verified by live teachersReduced fraction 3 / 2 Therefore, 3/2 simplified to lowest

How Do You Simplify 5 2 3 5 4 3 Socratic
Solution We know that rationalization factor for 3 2 2 3 and 3 2 are 3 2 2 3 and 3 2 respectively We will multiply numerator and denominator of the given expression 3 2 2 3 3 2 2 3 and 12 3 2 by 3 2 2 3 and 3 2 respectively, to getHere is the rule when a and b are not negative And here is how to use it Example simplify √12 12 is 4 times 3 √12 = √(4 × 3) Use the rule √(4 × 3) = √4 × √3 And the square root of 4 is 2 √4 × √3 = 2√3 So √12 is simpler as 2√3 Another example Example Simplify $\dfrac{2\left(\sqrt2 \sqrt6\right)}{3\sqrt{2\sqrt3}}$ The answer to this question is $\frac{4}{3}$ in a workbook How would I simplify $\sqrt{2\sqrt3}$ $?$ If it was something like $\ Stack Exchange Network Stack Exchange network consists of 1 Q&A communities including Stack Overflow, the largest, most trusted online community for
Simplify fully 2√3 x 3√8 Get the answers you need, now!Answer (Detailed Solution Below) Option 2 (62√3 96√2)75 India's Super Teachers for all govt exams Under One Roof FREE Demo Classes Available* Enroll For Free Now Detailed Solution Download Solution PDF Formula used= (√3–2√2) × (√32√2) b/z, (√32√2) is the rationalising factor of (√3–2√2) = (√3)² (2√2)² b/z, a²b² = 3 4 (2) = 3 8 = 5 Therefore, 5 is the answer for your problem Thank you ☺️ 65K views View upvotes View 1 share Answer requested by Varun Singla Related Answer Harish Chandra Rajpoot
Simplify (√3+2)(√3-2)のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | 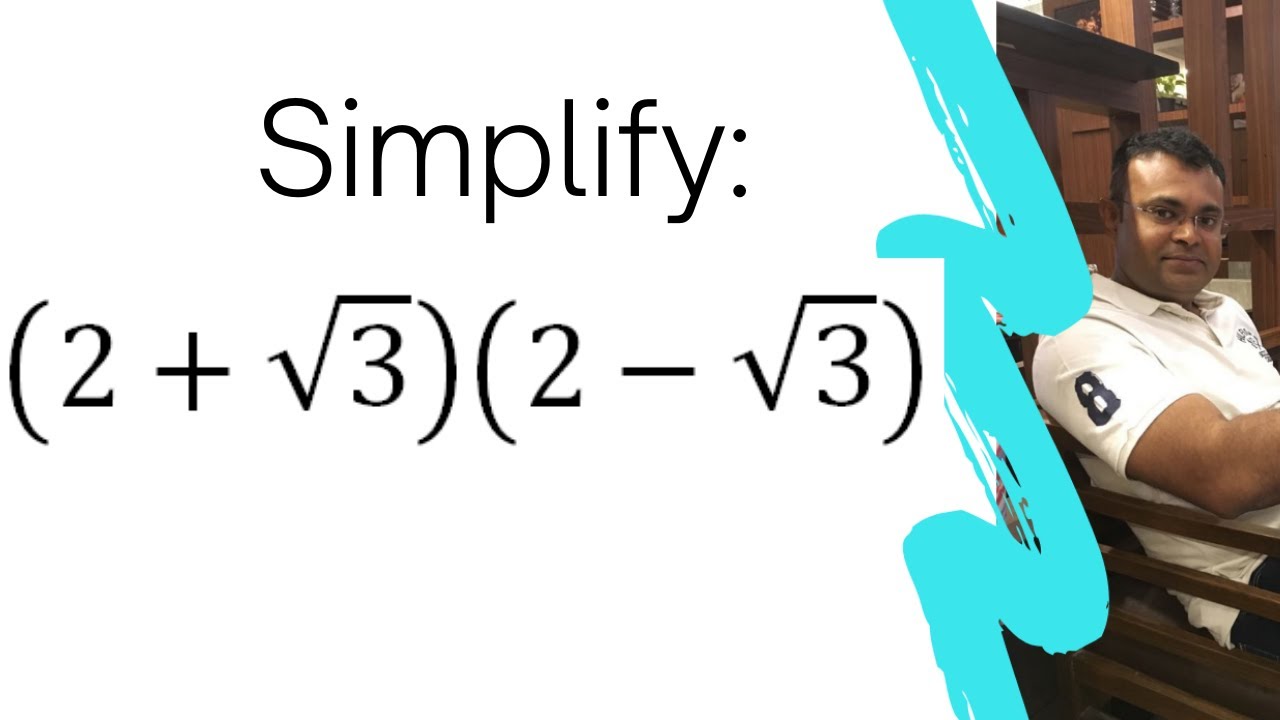 |  |
 |  | |
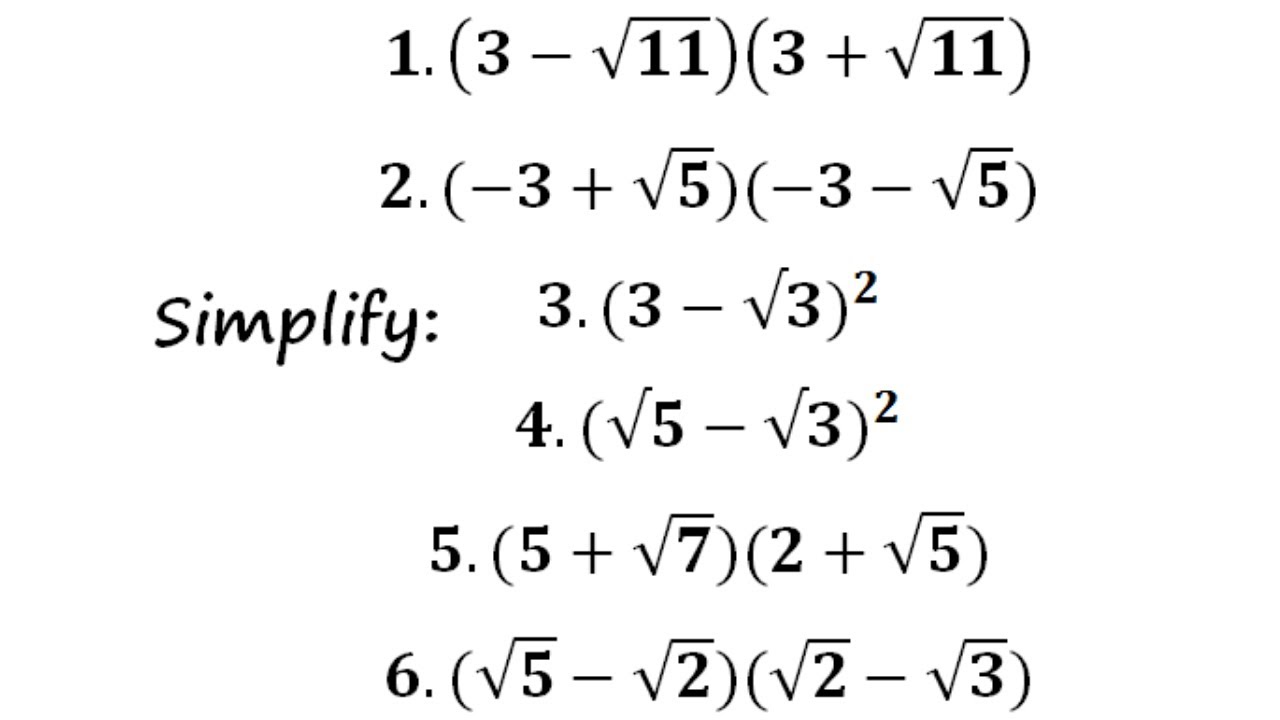 | 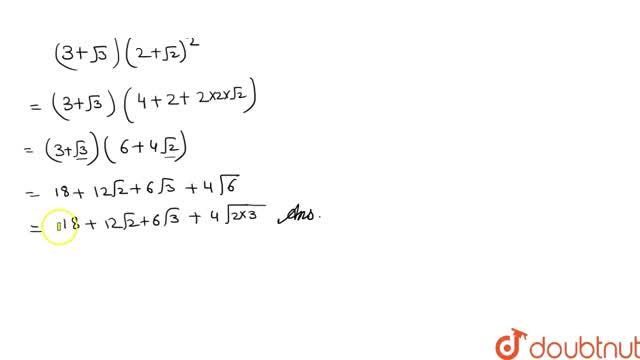 |  |
「Simplify (√3+2)(√3-2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
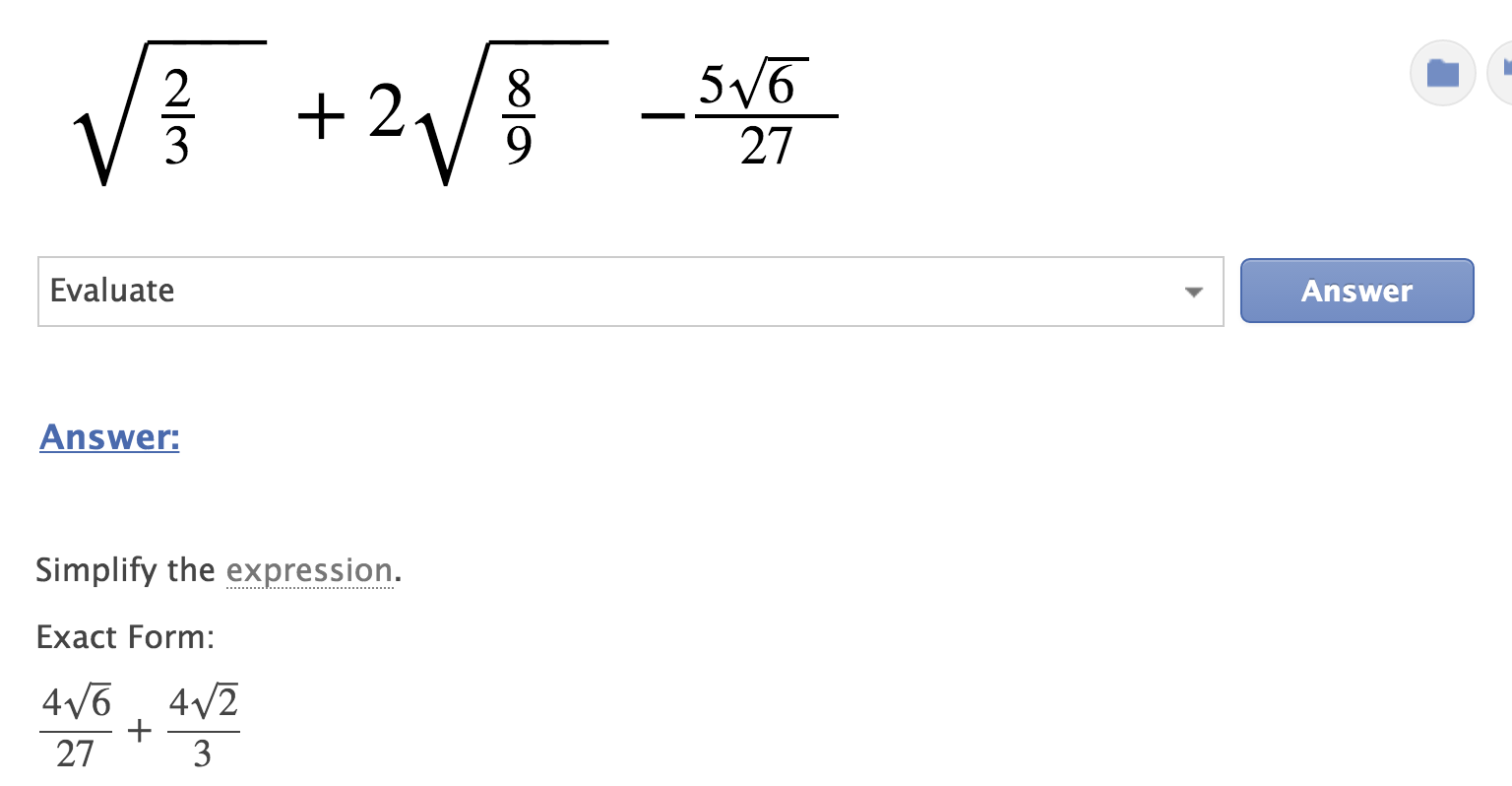 |  | |
 |  |  |
「Simplify (√3+2)(√3-2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 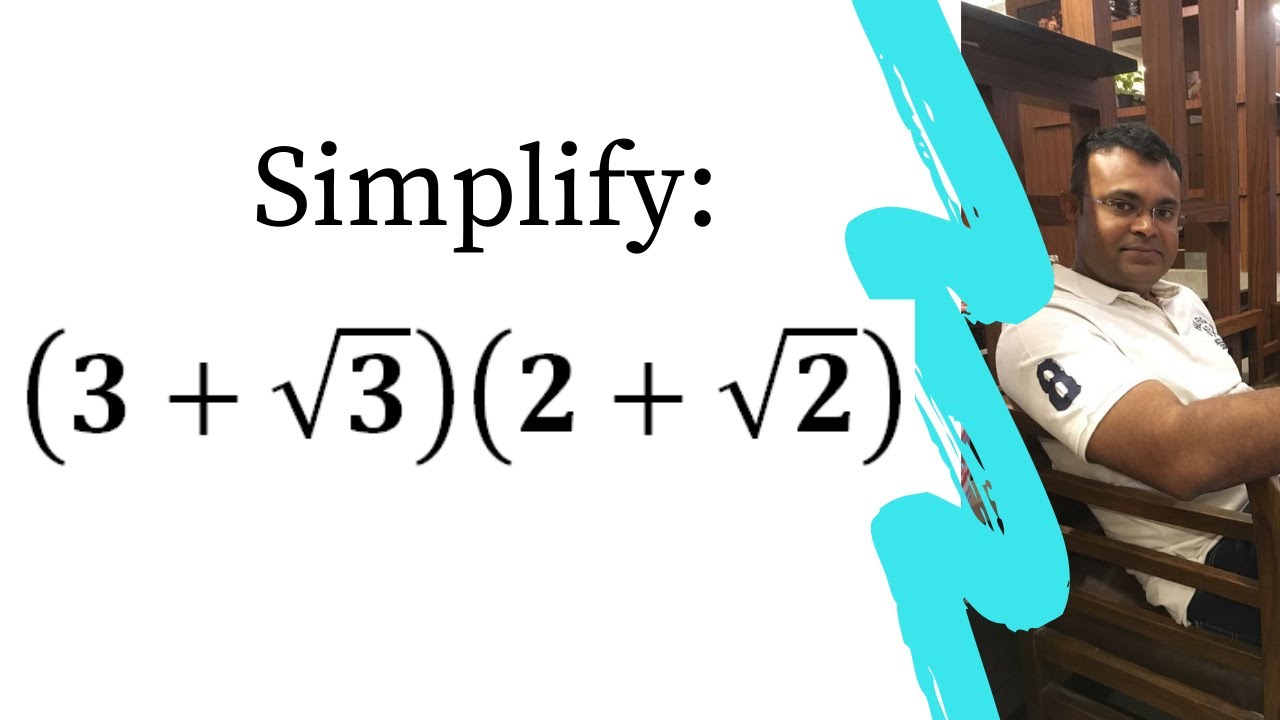 |  |
 |  |  |
 |  | |
「Simplify (√3+2)(√3-2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「Simplify (√3+2)(√3-2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「Simplify (√3+2)(√3-2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Simplify (√3+2)(√3-2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「Simplify (√3+2)(√3-2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Simplify (√3+2)(√3-2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「Simplify (√3+2)(√3-2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「Simplify (√3+2)(√3-2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「Simplify (√3+2)(√3-2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
How i solve the ncert class 9th solution of chapter number systems give me the solution of exercise 15 question number 2(1),(2) Find the best solution of this question by giving the simplest method of this question Simplify each of the following expressions (i) (3√3)(2√2) ,(ii) (3√3)(3√3 ) We can use here three formulas relating to exponents;




