30°、45°、60°の三角比の値は教科書で習いますが、今回は18°の三角比について考えてみます。 Ⅰ 18°の三角比の値 Ⅱ 求め方 Ⅲ 近似値 Ⅰ 18°の三角比の値 \(~18^{\ci三角比は,直角三角形の辺の比を表します。 長さがわからない辺があるので,まずは三平方の定理を利用してすべての辺の長さを求めましょう。 次に,定義に従って三角比の値をそれぞれ求めます。 今回の問題では が左下にあるので簡単に求められます。中学 数学 テクニック三角形の面積比を使っ 直角三角形の相似 相似の証明でも取り扱った「直角三角形の相似」です。 このページでは辺の長さや比を求めていきましょう。 相似な直角三角形が現れる図形として、最重要・最頻出のものを扱います! 直角である頂点から斜辺へ垂線をひくと

わかりやすい三角比と基本公式 Irohabook
三角 比 中学
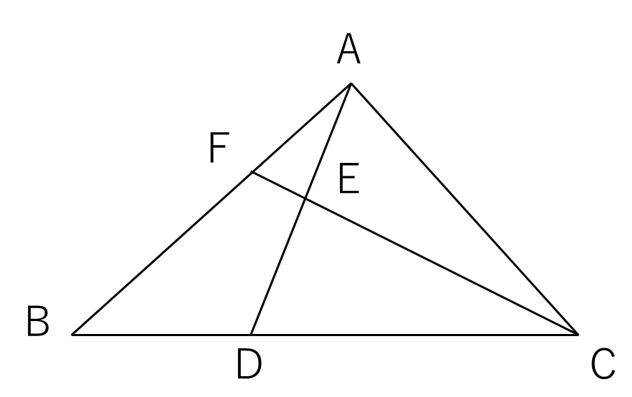
三角 比 中学- 三角形fadと三角形fdeはの面積比は、21。 二つの三角形の高さは同じなので、底辺の長さの比は21。 よって、adde=21 その流れで、今度は三角形faeと三角形feb。 面積比は31 高さは同じなので、底辺の長さの比は31。 よって、aeeb= 31 三角比 中学生Id 分类: 试题试卷 , 单元测试 , 上海 , 资源大小:378kb 资料简介 上海市建平中学19学年高一下学期 数学《三角比》单元测试卷 4 一填空题 1求值 ___ 2好きな言葉は「稠密」。どうもこんにちは、ジャムです。 今回は、受験で役に立つ有名角の三角比について紹介していきたい




复兴初级中学教科书三角 孔夫子旧书网
質問数学(中学):三角形と比の問題の解き方がわかりません 数学(中学), 質問(無料公開版(過去受付分)) 〔質問〕 三角形abcは∠abc=90度の直角三角形で、dは辺ab上の点で、ad:db=2:3である。 また、e、fはそれぞれの辺ac、線分adの中点で、gは線分dcとebとの交点である。ab=5cm、bc 三角形abe と 三角形abc の面積比も 1 : 3 になります。 <問題1 (2)の考え方と答え> いろいろな三角形の面積を比較しながら、最終的な面積の比較にもっていきます。 そこで、中学の復習ですが直角三角形の比について見ていきましょう。 (1) 3つの角が45°・45°・90°の直角三角形の3辺の長さの比は、 1 : 1 : √2 (2) 3つの角が30°・60°・90°の直角三角形の3辺の長さの比は、 1 : √3 : 2
三角比1(tanθ) 三角比2(sinθ,cosθ) 超重要 30°と60°の三角比;21年 6年生 入試解説 東京 男子校 面積比 ★★★★☆☆(中学入試難関校レベル) 印象に残った入試問題の良問を「今年の1問」と題して取り上げています。志望校への腕試しや,重要項目の確認に是非ご活用下さい。 id 山东省东平县斑鸠店镇中学数学(青岛版)九年级上册课件:21《锐角三角比》(共12张ppt) 预览 收藏 点击下载 加入资源篮 免费 教材: 数学 >> 青岛版九年级上册 >> 第2章 解直角三角形 >> 21 锐角三角比
三角比とは? 三角比とは、長さの測量のために生み出された概念で、直角三角形の \(\bf{2}\) 辺の比を角度を使って表したものです。 直角三角形の場合、\(1\) つの鋭角の大きさを決めるとすべての角の大きさが決まり、辺の比も決まります。 三角比の値の覚え方 覚えておくべきθの値は、0°、30°、45°、60°、90°の5つです。 これを表にすると となります。 このまま覚えてもいいのですが、少し覚えずらいので このようにします。 こうすると、sinθ,cosθの値をすべて ( は0~4)の形で表す相似な2つの三角形 相似な2つの三角形 ABCと A'B'C'があります。(相似比は1:k) ABCの各辺の長さをa、b、cとしたときに A'B'C'の各辺の長さはka、kb、kcとなります。 このとき、2つの三角形の面積比についてみてみましょ




国立宜兰高级中学 维基百科 自由的百科全书




广东最难进的七所中学 六所在珠三角 一所比一所牛 都是顶尖的 每日头条
中学数学。 三角形と比の基礎。 中学数学。 三角形と比の基礎。 If playback doesn't begin shortly, try restarting your device Videos you watch may be added 平面図形 長さの比、面積比の問題 どう指導しますか? 左の図の三角形ABCで、AEEC=21,BDDC=45です。 これについて、次の問いに答えなさい。 (1) AFFDを求めなさい。 (2) 四角形FDCEと三角形ABCの面積の比を求めなさい。 平面マスター 解答日時「第513回 女子中の平面図形 3」 前回は、中学入試の中から女子中で出された「平面図形」の問題について、「求積(面積を求める問題)」の1行問題を見ましたが、今回取り扱うテーマは、 「辺の比と面積比」の大問形式の問題 です。 ご紹介する問題では、「平面図形と比」で学習する「高さ







数学中考知识点总结10 相似形 中考数学 沪江中学学科网
中学生からの質問(数学) や が出てくるのは,次の2つの特別な直角三角形の場合です。 直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°,60°,90°の 中学生向け 数学三平方の定理が成り立つ三辺の比:最重要7パターン ~受験の秒殺テク(5)~ 絶対におぼえておきたい直角三角形top7 高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる"秒殺テクニック"を紹介していきます。 映像授業を視聴すること 90°/60°/30°の三角定規は最も短い辺と長い辺の比は1:2 90°/45°/45°の三角定規は長い辺を底辺とすると「高さ」と「底辺」の比は1:2 ↓ ↓ 中学入試の算数受検問題上のポイント! 1 「30°」「60°」「45°」という数字を見たら比の利用を考える 2 「30°」なくても自分で作れないかを考える(150°、135°、1°でピンと来る!) 90°/60°/30°の三角定規は最も



数i 基本的な三角比の値
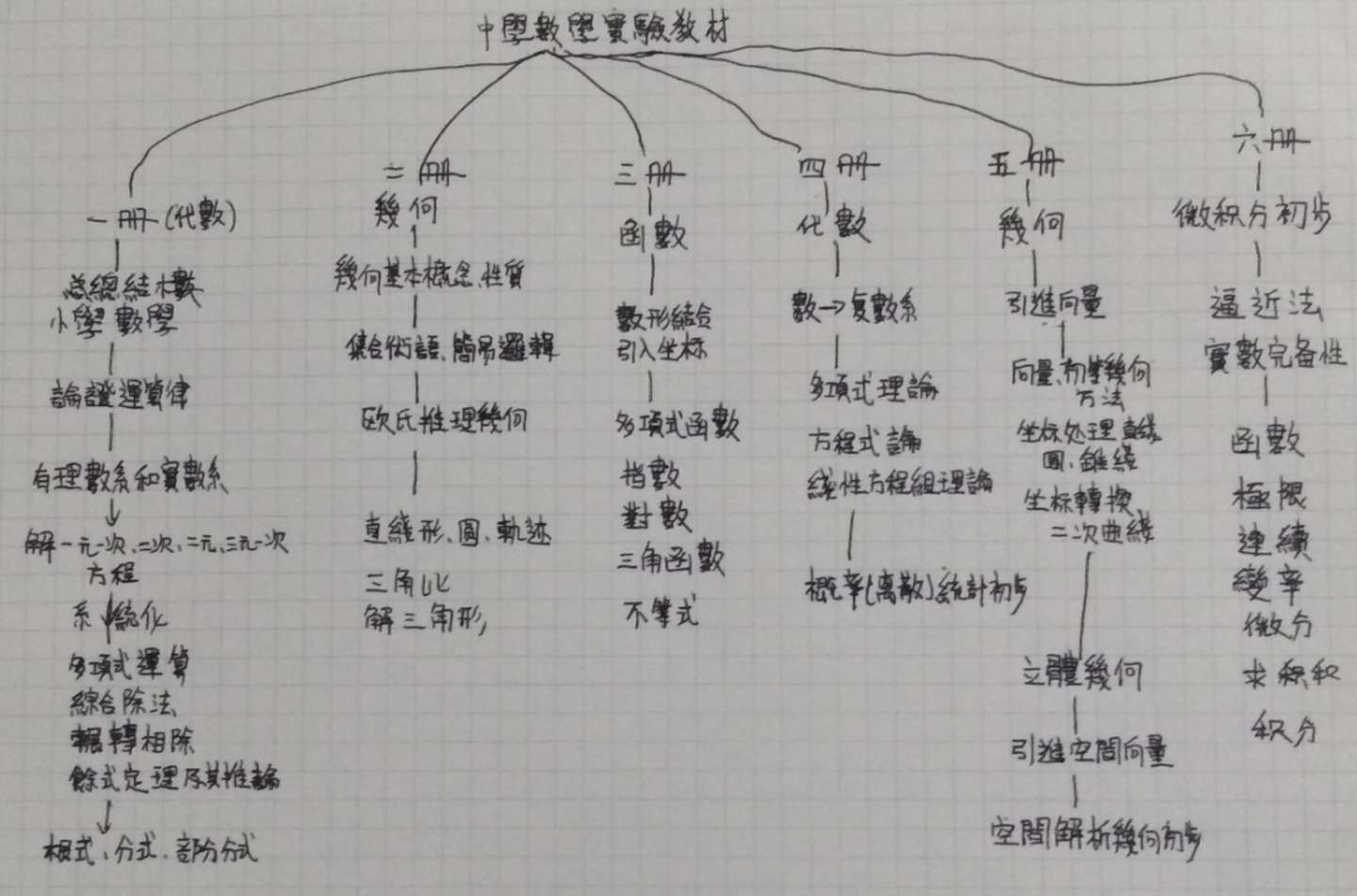



中学教材版本 中学教材目录 中学教材课程 知乎
三角比とは何か 簡単に言ってしまえば、 三角比とは、直角三角形の各辺の長さの比を表したもの です。 なかなか言葉ではわかりにくいのですが、よく測量(ある点とある点の距離を測ること)などで使われる計算式くらいに覚えておきましょう。数学三角錐の体積比を楽に求められる公式 ~受験の秒殺テク(2)~ キーワードは"ちぢみ率" 高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる"秒殺テクニック"を紹介していきます。高校数学Ⅰで学習する三角比の単元から 「三角比を含む方程式の解き方」 について解説していきます。 この記事は、数学がニガテという方に向けて解き方の手順をイチから解説していきます。 以下の問題を取り上げて、 三角比 数学Ⅰ36°の三角比、二等辺三角形を用いて求める方法




美国中学课程介绍 美国中学课程辅导篇




锐角三角比基础复习 楠木轩
三角比の式の値は入試や模試などでよく見かける問題です。 和、差が与えられているときには両辺を2乗して積を求めることができる。 この考え方と式の変形について覚えておけば楽勝な問題です。 サクッと解けるように練習しておいてくださいね(/・ω・)/ 第五章 三角比资料优选沪教版(上海)高中数学高一第二学期数学学科网 学科网 > 高中数学 > 教材同步 > 沪教版(上海) > 高一第二学期 > 第五章 三角比 > 资料列表 历年真题 竞赛 重置筛选条件 类 别: 不限 试题试卷 教案 课件 素材 音视频 备课综合 学 45°の三角形は直角 二等辺三角形 として知られています。 一般的な二組の三角定規の片方の三角形でもあります。 そんな、45°の三角比は、 1 1 √2 45°の直角三角形が 二等辺三角形 であることを踏まえれば、 三平方の定理 を使って容易に求めることができます。 AB = 1 とすると、 ABC は 二等辺三角形 なので、 AC = 1 三平方の定理 より、 AB2 AC2 = BC2



18中国大陆出国留学最强中学top100榜出炉 最牛大数据 英国精英大学




锐角三角比基础复习 楠木轩
黄冈中学高考备考笔记52(1)任意角的三角比(上课稿)doc,PAGE PAGE 1 §52(1) 任意角的三角比 任意角的三角比、单位圆 教学过程: 一、情景引入 回顾:在初中我们学习了锐角的三角比,它是在直角三角形的条件下,通过角的对边、邻边与斜边之间两两的比值来定义的例如: 引入:前面θの範囲に注意して図をイメージ 三角比の値から角度を求める問題が出てきたら、直角三角形の図をイメージしよう。 sinθ=(高さ)/(斜辺) cosθ=(底辺)/(斜辺) tanθ=(高さ)/(底辺) の関係から、直角三角形をイメージすれば、角度θが求められるね。 そして θの範囲 にも注目しよう。 0°≦θ≦180° のときは、 座標平面の上半分 、 分度器 の範囲で ここでは数学1の「三角比」についてまとめています。三角比は数学2で学習する三角関数の基礎でありつつ、単元を問わず広く利用されていますので、しっかり学習しておきましょう。 学校や塾では教えてくれない、元塾講師の思考回路の公開 基礎知識 三角比三角比のまとめ b




平面図形をマスター 三角形の面積比 応用編その3




数学ia 三角比とは何か 定義を明らかにしつつ三角比の問題を解く Himokuri



圣大卫中学st Davids School 留学美国网




高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト
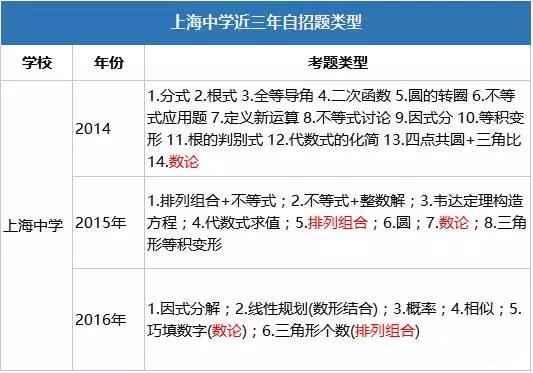



17年四校自招都考些什么 内含四校近三年题型 知乎




中学知识 Cot是什么 教育新闻网



聊城文轩中学小升初考试数学试题 聊城小升初 奥数网



成都94中学的问题比出事的49中严重多了 华人论坛丫丫的港湾小说股坛海外华人yayabay Com 全球华人



市西实验中学初三数学月考卷 中考数学 上海中考网




京华中学初三辅导班资料7 解直角三角函 九年级下 数学 教案 优优课件
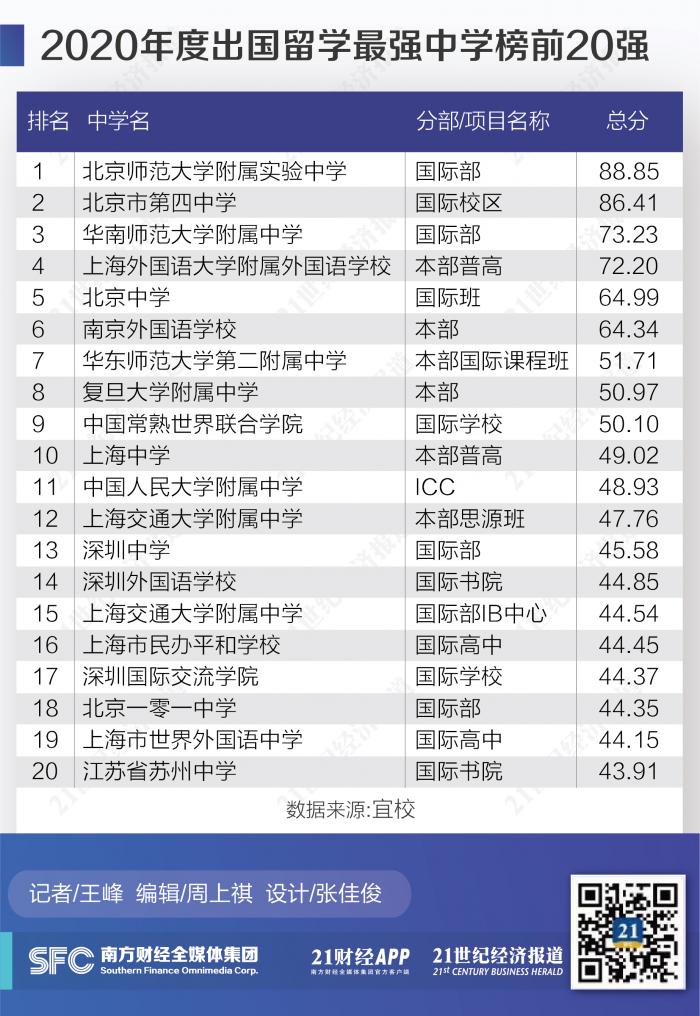



国际学校排行榜 这些学校 收割 最多海外名校offer 21经济网




6park Com 复旦大学副教授晒工资到手00 还不如中学老师




わかりやすい三角比と基本公式 Irohabook




复兴初级中学教科书三角 孔夫子旧书网




Etv 中學數學科 三角比 03 Youtube



Studydoctor相似な三角形の辺の比 中3数学 Studydoctor




谁才是深圳最好中学 21年深圳所中学高考喜报 附近几年喜报和录取率 掘金圈
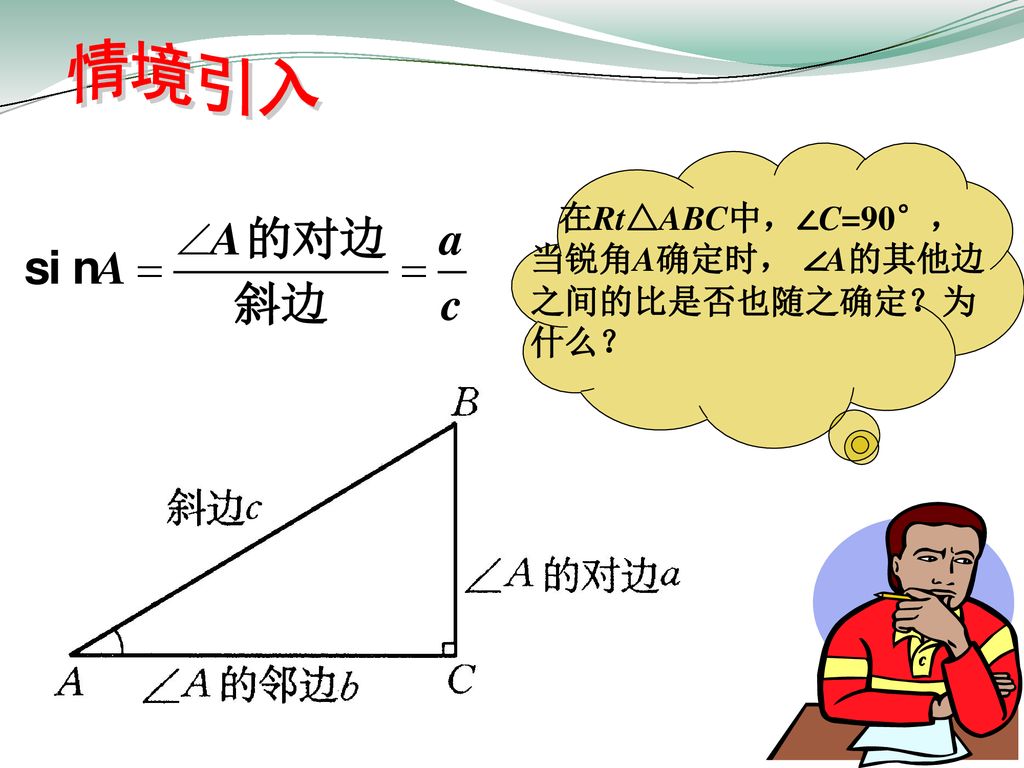



义务教育课程标准实验教科书九年级下册将军县 兴国28 1锐角三角函数 第2课时 兴国县潋江中学赖华丹 Ppt Download



测试发布图文 校园风貌 万宁市第二中学




Pdf 袁智强 交叉融合的stem教育 背景 内涵与展望 19no3教育研究与评论 中学教育教学



合江中学与东方学校合作办学助力城乡义务教育均衡发展




初一数学 19 年上海市浦东新区建平中学期末试卷




各类教育文章分享 中学数学术语中英对照 分类整理




三角比 30 45 60 もう一度やり直しの算数 数学




中学数学 覚えておくと得する三角比 ジャムと愉快な仲間たち 0名




广德中学21高考成绩出炉 文理科 网易订阅




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



三角函数练习题相比起三角函数这款自主suv更容易让人记住 尚书坊




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su



360影视 影视搜索



Tan是什么边比什么边 初三网



三角函数毕业论文正文 沃文网wodocx Com



英国公立中学gcse排行top100 你选对学校了吗 A加未来国际教育




衡水中学 教师版 高中数学知识点归纳总结 最全整理 知乎




Ppt 总复习powerpoint Presentation Free Download Id



玩转初中几何 等边三角形衍生问题的多种解法探究 中学数学研究会 微信公众号文章阅读 Wemp




平江张市中学 上门送课带 干货 结对帮扶授真经 教学 教研 示范课 老师 网易订阅




广东最难进的七所中学 六所在珠三角 一所比一所牛 都是顶尖的 每日头条




高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト




辽宁省瓦房店市第八初级中学九年级数学下册 28 1 锐角三角函数 教学设计3 新人教版下载 Word模板 爱问共享资料




继续井喷 英国私校全面涌入中国 疫情下再开16家 知乎



广州中学数学之窗 青春网站建设工作室 龙游网站建设 龙游网站制作 龙游网站设计 学校网站 政府网站 企业网站 网站模板



第一章直角三角形的边角关系第一节从梯子的倾斜程度谈起 二 广东省深圳市翠园中学初中部李秀英 Ppt Download




河北省抚宁县第六中学高中数学任意角的三角函数2教案新人教a版必修4下载 Word模板 爱问共享资料



初中数学 圆幂定理与相似比 中学数学研究会 微信公众号文章阅读 Wemp



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



陆家嘴 豪门 学校 进才中学 昂迪教育



上海市徐汇中学21年初中招生简章公布 课程



高中数学 交附 进才周练 单元测试卷 作业



数i 基本的な三角比の値




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



英国公立中学gcse排行top100 你选对学校了吗 A加未来国际教育




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



上海市上宝中学初三上学期数学期中考试 资料




英国留学 中学入学考什么 洛阳新东方前途出国




岳云中学 维基百科 自由的百科全书




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




谁才是深圳最好中学 21年深圳所中学高考喜报 附近几年喜报和录取率 掘金圈



25 2求锐角的三角比的值 哔哩哔哩 つロ干杯 Bilibili




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月



25 3解直角三角形 哔哩哔哩 つロ干杯 Bilibili



初中数学 圆幂定理与相似比 中学数学研究会 微信公众号文章阅读 Wemp




中学数学 覚えておくと得する三角比 ジャムと愉快な仲間たち 0名
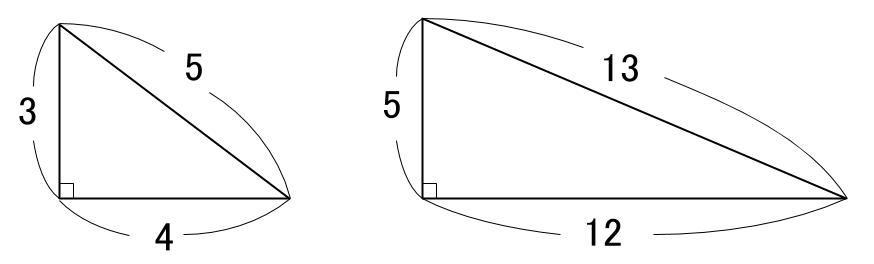



中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su



市油田第六中学在省录像课比赛活动中获佳绩 河南省濮阳市油田第六中学



25 4解直角三角形的应用 哔哩哔哩 つロ干杯 Bilibili




三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ




中学 数学 テクニック 三角形の面積比を使って辺の比を出す 高校入試 高校受験 裏ワザ Youtube




广东最难进的七所中学 六所在珠三角 一所比一所牛 都是顶尖的 每日头条



初中数学 圆幂定理与相似比 中学数学研究会 微信公众号文章阅读 Wemp




年高一下建平三角比测试典型题解析 8题 哔哩哔哩 Bilibili




古来县校际华语辩论赛 古来福建公会青年团 Inicio Facebook



初三上锐角三角比单元练习测试题 中考数学 上海中考网



高中学霸的情书被截获 学渣表示看不懂 老师看完被感动 育儿资讯 娱乐新闻网




中3数学 有名角と比 映像授業のtry It トライイット
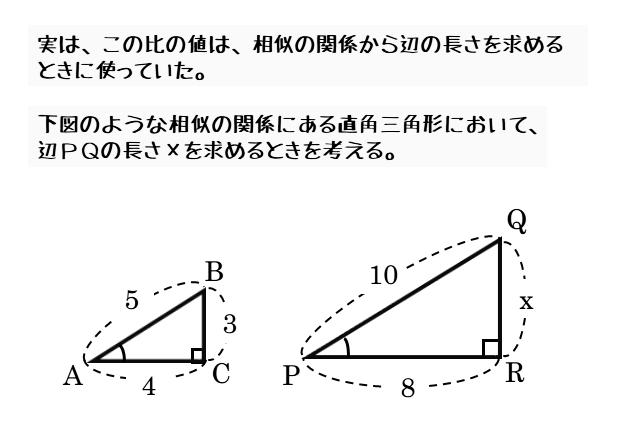



図形と計量 三角比の定義について 日々是鍛錬 ひびこれたんれん



真榜 最新资讯



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ
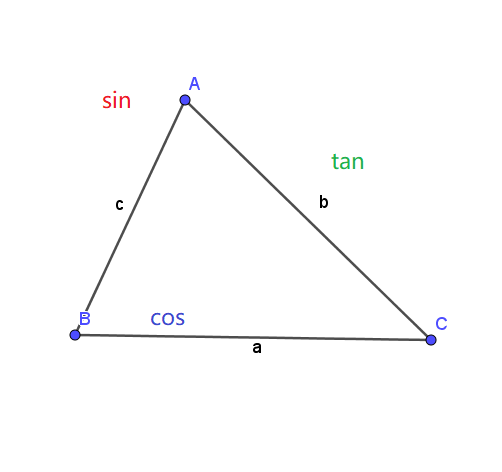



三角形中三角比的特殊公式 知乎



陆家嘴 豪门 学校 进才中学 昂迪教育



高中数学 衡水中学公式口诀丨八大专项提分秘籍 高考轻松提分 教育资讯 早游戏



中3 数学相似比 ニスヌーピー壁紙




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



8 面積比の6パターン って 中学受験ドクター Youtube




广东省前三的深圳中学 今年一个班51人考上一流名校 清华 高中 中学 深圳中学 深圳外国语学校 名校 手机网易网



成都94中学的问题比出事的49中严重多了 华人论坛丫丫的港湾小说股坛海外华人yayabay Com 全球华人




除了珠三角 广东其他地区教师工资其实不算高 地区差异比较大 教龄 工龄 公积金 网易订阅



高一下学期期中复习讲义 三角比至三角函数 Pan
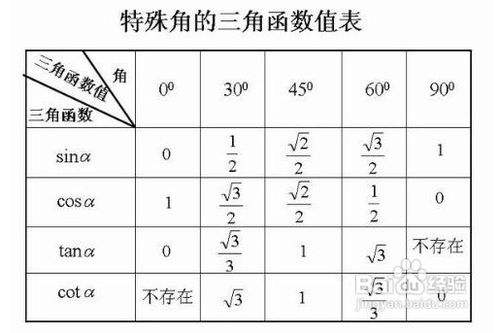



初中三角函数的知识点有哪些 怎么学习 百度经验



中学数学 三角比 Excellent仕事術


